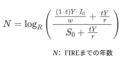背景：『4%ルール』とは？

4%ルールとは、「毎年資産の4%以内で生活費を引き出せば、資産が尽きずに生活できる」という考え方です。

FIREの目標資産額は次のように計算されます：

\[ \text{必要資産額} = \text{年間支出} \times \frac{1}{0.04} \]

📌 なぜこの式になるのか（導出の流れ）

① FIRE達成時の資産額

FIREを達成するには、資産からの取り崩しだけで生活費をまかなう必要があります。年間支出は：

\[ \text{年間支出} = \text{収入} \times (1 – t) \]

したがって、必要資産額は：

\[ \text{必要資産額} = \frac{\text{収入} \times (1 – t)}{0.04} \]

② 複利運用の資産増加

資産は以下の2つで毎年増えます。

  • 新たな貯蓄：収入 × \( t \)
  • 資産運用益：資産 × \( r \)

毎年の積立額が一定である場合、資産は複利で増えていきます。N年間の積立を考えると：

  • 1年目の積立：\( \text{年間貯蓄額} \times (1+r)^{N-1} \)
  • 2年目の積立：\( \text{年間貯蓄額} \times (1+r)^{N-2} \)
  • 3年目の積立：\( \text{年間貯蓄額} \times (1+r)^{N-3} \)

以下略。これを最後まで書くと：

\[ \text{必要資産額} = \text{年間貯蓄額} \cdot (1+r)^{N-1} + \cdots + \text{年間貯蓄額} \cdot (1+r)^0 \]

これを因数分解して整理すると：

\[ \text{必要資産額} = \text{年間貯蓄額} \times \left[ (1+r)^{N-1} + (1+r)^{N-2} + \cdots + 1 \right] \]

カッコ内は 等比数列の和です。

公式：

\[ a + ar + ar^2 + \dots + ar^{n-1} = a \cdot \frac{r^n – 1}{r – 1} \]

ここでは：

  • 初項 \( a = 1 \)
  • 公比 \( = 1 + r \)
  • 項数 \( = N \)

したがって：

\[ \frac{(1 + r)^N – 1}{r} \]

となります。つまり：

\[ (1+r)^{N-1} + (1+r)^{N-2} + \cdots + 1 = \frac{(1+r)^N – 1}{r} \]

複利の資産成長式は：

\[ \text{必要資産額} = \text{年間貯蓄額} \times \frac{(1 + r)^N – 1}{r} \]

年間貯蓄額 \( = \text{収入} \times t \) を代入：

\[ \frac{\text{収入}(1 – t)}{0.04} = \text{収入} \times t \times \frac{(1 + r)^N – 1}{r} \]

収入を両辺で約分：

\[ \frac{1 – t}{0.04} = t \times \frac{(1 + r)^N – 1}{r} \]

③ 上の式を \( N \) について整理する

まず両辺を整理します：

\[ \frac{(1 + r)^N – 1}{r} = \frac{1 – t}{0.04 t} \]

両辺に \( r \) をかけて \( 1 \) を足します：

\[ (1 + r)^N = \frac{r(1 – t)}{0.04 t} + 1 \]

そして対数をとると：

\[ N = \log_{1 + r}\left(\frac{r}{0.04} \cdot \frac{1 – t}{t} + 1\right) \]

式の直感的な意味

  • \( \frac{1 – t}{t} \)：支出と貯蓄のバランス。大きいとFIREは遠のく
  • \( \frac{r}{0.04} \)：運用益と引き出し率の比。高いとFIREが近づく
  • \( \log \)：複利による資産成長を「年数」に変換している

まとめ

  • この式は「4%ルール」と複利運用をベースに導出されている
  • 貯蓄率と年利の2つだけでFIRE年数を計算可能
  • 収入金額や資産額は含まれていない（モデルとして簡易化されている）

この導出を理解しておけば、自分にとってのFIRE戦略を論理的に立てやすくなります。ぜひ活用してみてください。 また、現時点での資産額やサイドFIRE時の収入を含めて計算をしようと思うと、貯蓄率の中身である年間収入と年間支出に分解して計算する必要があります。そちらについても別途記事にする予定です。